A. Dasar analisis
Bagian ini memberikan dasar teoritis yang diperlukan untuk menggunakan COSMOSWorks, menjelaskan analisis, asumsi dan dasar hasil prediksi. Bagian ini juga sempat menjelaskan bagaimana melakukan analisis.
Anda tidak harus memutuskan masalah yang desain hanya berdasarkan hasil perhitungan COSMOSWorks. Penggunaan hasil ini dengan data eksperimen dan pengalaman praktis. Hanya percobaan baru membuat desain Anda berlaku. COSMOSWorks membantu Anda menghemat waktu dan biaya dengan mengurangi jumlah eksperimen daripada penghapusan eksperimental.
Kami akan membahas isu-isu berikut:
Analisis statis linear
Ketika gaya luar yang bekerja pada objek, objek ini akan berubah bentuk dan gaya akan melewati seluruh organisme. pasukan asing akan menimbulkan stress dan jet untuk meletakkan segala sesuatu kembali ke keseimbangan.
Penelitian statis linear menghitung perpindahan, strain, stress dan jet bawah tindakan kekuatan eksternal.
studi Linear statis dilakukan berdasarkan asumsi sebagai berikut:
Dengan asumsi statis: Semua stres bertindak perlahan dan bertahap meningkat sampai mencapai kekuatan penuh. Setelah mencapai kekuatan penuh, kekuatan akan terus konstan dari waktu ke waktu. Asumsi ini memungkinkan kita untuk mengabaikan inersia dan redaman karena percepatan dan kecepatan kecil, gaya adalah diabaikan.
Dimana kekuatan diterapkan untuk berubah seiring waktu, dapat menyebabkan kekuatan kejutan inersia atau besar, kami telah menghitung analisis dinamis. Perubahan beban dinamis dari waktu ke waktu dan dalam banyak kasus menyebabkan gaya inersia atau kejutan besar tidak bisa diabaikan bukan asumsi statis diterapkan.
Catatan:
Dengan asumsi linier: Hubungan antara beban dan respon yang dihasilkan (Pemindahan, strain dan stres) adalah linier. Misalnya, jika Anda dua kali lipat meningkatkan beban, respon model juga dua kali lipat. Anda dapat melakukan analisis dengan asumsi linear jika:
Beberapa dasar definisi
Tegangan di dalam material akan berubah dari satu titik ke titik lain. Melalui setiap area yang kecil, gaya dampak dari sisi ke sisi daerah ini. Stres adalah ukuran untuk menentukan intensitas tegangan ini (gaya per satuan luas).
Stres pertama kali dihitung dalam fitur, yang dikenal sebagai poin atau Gauss Quadrature, yang terletak di setiap elemen. Titik-titik yang dipilih untuk mengoptimalkan jumlah hasil. Program ini akan menghitung tegangan pada nodus setiap elemen dengan ekstrapolasi hasil yang tersedia pada titik-titik Gauss.
Setelah menjalankan analisa berhasil, hasil dari tegangan pada setiap node elemen setiap node sudah ada di database. node umum dari dua atau lebih elemen akan memiliki hasil yang lebih. Secara keseluruhan, hasil ini tidak identik karena metode elemen hingga merupakan metode perkiraan. Misalnya, jika ada tombol yang umum untuk tiga unsur, dapat memiliki tiga stres nilai sedikit berbeda untuk setiap komponen tegangan pada titik ini.
Saat melihat hasil stres, Anda mungkin perlu mengetahui stres atau node elemen stres. Untuk menghitung elemen stres, program akan menghitung nilai tegangan rata-rata node dalam elemen ini. Untuk menghitung tombol stres, program akan menghitung rata-rata hasil yang sesuai dari semua elemen yang berbagi node.
Berikut contoh gambar beberapa hasil uji komponen material berbeda dengan presure nilai satuan newton (n).
sumber meslab.org
Bagian ini memberikan dasar teoritis yang diperlukan untuk menggunakan COSMOSWorks, menjelaskan analisis, asumsi dan dasar hasil prediksi. Bagian ini juga sempat menjelaskan bagaimana melakukan analisis.
Anda tidak harus memutuskan masalah yang desain hanya berdasarkan hasil perhitungan COSMOSWorks. Penggunaan hasil ini dengan data eksperimen dan pengalaman praktis. Hanya percobaan baru membuat desain Anda berlaku. COSMOSWorks membantu Anda menghemat waktu dan biaya dengan mengurangi jumlah eksperimen daripada penghapusan eksperimental.
Kami akan membahas isu-isu berikut:
Analisis statis linear
Ketika gaya luar yang bekerja pada objek, objek ini akan berubah bentuk dan gaya akan melewati seluruh organisme. pasukan asing akan menimbulkan stress dan jet untuk meletakkan segala sesuatu kembali ke keseimbangan.
Penelitian statis linear menghitung perpindahan, strain, stress dan jet bawah tindakan kekuatan eksternal.
studi Linear statis dilakukan berdasarkan asumsi sebagai berikut:
Dengan asumsi statis: Semua stres bertindak perlahan dan bertahap meningkat sampai mencapai kekuatan penuh. Setelah mencapai kekuatan penuh, kekuatan akan terus konstan dari waktu ke waktu. Asumsi ini memungkinkan kita untuk mengabaikan inersia dan redaman karena percepatan dan kecepatan kecil, gaya adalah diabaikan.
Dimana kekuatan diterapkan untuk berubah seiring waktu, dapat menyebabkan kekuatan kejutan inersia atau besar, kami telah menghitung analisis dinamis. Perubahan beban dinamis dari waktu ke waktu dan dalam banyak kasus menyebabkan gaya inersia atau kejutan besar tidak bisa diabaikan bukan asumsi statis diterapkan.
Catatan:
- Penentuan beban diterapkan dengan asumsi statis atau tidak adalah sangat penting, alasan adalah beban dinamis dapat menyebabkan stres yang lebih besar dari 1 / (2x) kali beban statis dengan kekuatan yang sama, di sini, x adalah koefisien redaman. Dengan sedikit redaman struktur, misalnya dengan 5% redaman, stres akan lebih besar dari 10 kali tegangan statis. kasus terburuk adalah resonansi. [1]
- Anda dapat menggunakan analisis statik untuk menghitung respon struktur benda berputar dengan kecepatan konstan atau bergerak lurus dengan percepatan konstan, gaya inersia yang dihasilkan oleh konstan dari waktu ke waktu.
- Anda dapat menggunakan modul analisis Respon Dinamis atau Dinamik nonlinier, Dalam produk COSMOS lain, untuk menghitung struktur load-bearing. Download meliputi kekuatan fluktuasi, dan tabrakan acak. COSMOSWorks 2006 tanpa modul ini.
Dengan asumsi linier: Hubungan antara beban dan respon yang dihasilkan (Pemindahan, strain dan stres) adalah linier. Misalnya, jika Anda dua kali lipat meningkatkan beban, respon model juga dua kali lipat. Anda dapat melakukan analisis dengan asumsi linear jika:
- Semua materi dalam model untuk mengikuti hukum Hooke, bahwa rasio tegangan dengan tingkat regangan. (Kita tahu bahwa stres adalah bukan realitas, sebagian besar dengan tingkat regangan, tetapi hanya perkiraan itu. Asumsi ini menyederhanakan perhitungan dan hasilnya tidak perbedaan yang signifikan dengan percobaan).
- Perpindahan yang dihasilkan cukup kecil untuk mengabaikan perubahan kekerasan akibat beban. (Kekakuan struktur tergantung pada bentuk struktur. Ketika struktur beban bentuknya akan berubah, diekspresikan melalui perpindahan, defleksi dan rotasi. Dengan demikian, umumnya kekakuan struktur akan berubah ketika memuat perhitungan rinci Tetapi jika masalah tersebut menjadi lebih kompleks. Asumsi ini menyederhanakan masalah bagi kasus-kasus hanya struktur perpindahan kecil. di bawah pengaruh kekuatan asing).
- Batas kondisi tidak berubah selama pembebanan. beban Konstan harus sama dalam kekuatan, arah dan distribusi. Kami tidak berubah bila deformasi model. (Termasuk kondisi batas dan beban untuk hambatan struktural, seperti engsel, tekuk, panas ... Asumsi ini juga menyederhanakan perhitungan yang sebenarnya, tetapi tidak pernah seperti ini, kita harus mengubah mengubah pola deformasi.)
Beberapa dasar definisi
Tegangan di dalam material akan berubah dari satu titik ke titik lain. Melalui setiap area yang kecil, gaya dampak dari sisi ke sisi daerah ini. Stres adalah ukuran untuk menentukan intensitas tegangan ini (gaya per satuan luas).
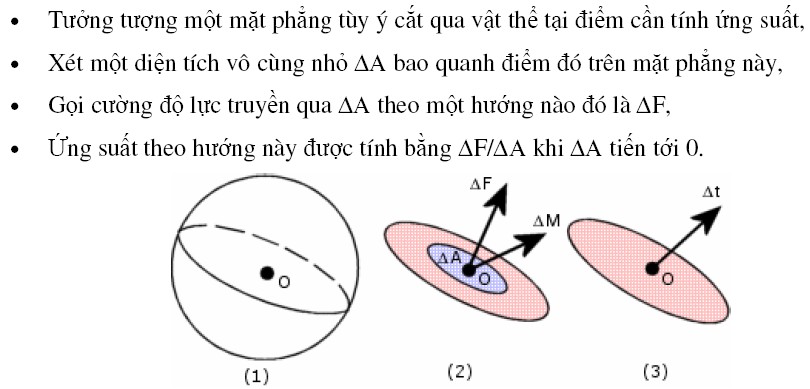
- Stress (stres). Dalam objek terus menerus, Anda dapat menghitung tegangan pada titik sebagai berikut:
- Bayangkan sebuah pesawat sewenang-wenang memotong melalui materi pada titik-titik stres,
- Pertimbangkan daerah yang sangat kecil DeltaA sekitar titik ini dalam pesawat, (tidak mengizinkan memasukkan karakter Yunani itu?)
- Call kekuatan dikirimkan intensitas DeltaA dalam arah yang DeltaF,
- Stres dalam arah ini dihitung dengan DeltaF /DeltaA ketika DeltaA ke 0.
- Strain (regangan)Ketegangan ini. Persentase perubahan panjang d L pada panjang aslinya L. Ketegangan adalah berdimensi kuantitas.
- Rantai perhitungan A model grid, dengan satu set perpindahan wajib dan beban, programanalisis statis linear akan lanjutkan sebagai berikut:
- Program ini akan membangun dan memecahkan sistem persamaan keseimbangan elemen hingga linier untuk perpindahan pada setiap node.
- Kemudian, program ini akan menggunakan hasil ini untuk menghitung perpindahan ketegangan komponen.
- Akhirnya, program ini menggunakan hasil ketegangan ketegangan dan stres terkait untuk menghitung stres.
Stres pertama kali dihitung dalam fitur, yang dikenal sebagai poin atau Gauss Quadrature, yang terletak di setiap elemen. Titik-titik yang dipilih untuk mengoptimalkan jumlah hasil. Program ini akan menghitung tegangan pada nodus setiap elemen dengan ekstrapolasi hasil yang tersedia pada titik-titik Gauss.
Setelah menjalankan analisa berhasil, hasil dari tegangan pada setiap node elemen setiap node sudah ada di database. node umum dari dua atau lebih elemen akan memiliki hasil yang lebih. Secara keseluruhan, hasil ini tidak identik karena metode elemen hingga merupakan metode perkiraan. Misalnya, jika ada tombol yang umum untuk tiga unsur, dapat memiliki tiga stres nilai sedikit berbeda untuk setiap komponen tegangan pada titik ini.
Saat melihat hasil stres, Anda mungkin perlu mengetahui stres atau node elemen stres. Untuk menghitung elemen stres, program akan menghitung nilai tegangan rata-rata node dalam elemen ini. Untuk menghitung tombol stres, program akan menghitung rata-rata hasil yang sesuai dari semua elemen yang berbagi node.
Berikut contoh gambar beberapa hasil uji komponen material berbeda dengan presure nilai satuan newton (n).
sumber meslab.org



Tidak ada komentar:
Posting Komentar